Counter采集过来的整数数据increase后出现小数点的数据
情况如下图所示:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QJllj7Bm-1618565129865)(/img/bVbLF9H)]](http://static.itsharecircle.com/231028/66560cbb793672d37773f8f33c8eb953.png)
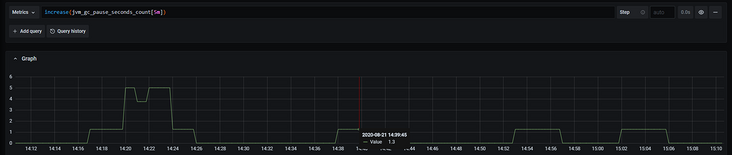
increase(jvm_gc_pause_seconds_count[5m])在Grafana Explore中查询出来的数据存在小数点,什么鬼,increase难道不是两个数据的差值吗,两个整数相减为什么会有小数点呢???这你让我怎么跟leader交代。。。
查询SQL:
increase(jvm_gc_pause_seconds_count{instance="$instance", application="$application"}[5m])
increase()函数实现的源代码分析:
在源码里就找到了一个extrapolatedRate()的函数
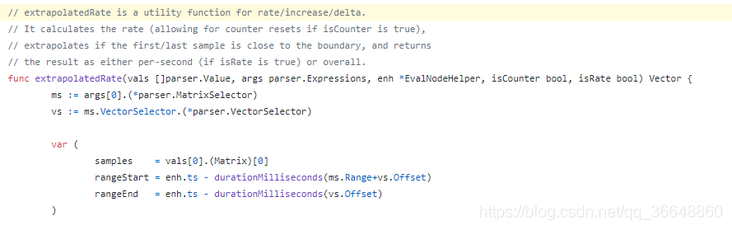
源码中的注释
extrapolatedRate is a utility function for rate/increase/delta.
意思是这rate/increase/delta三种函数的公用实现函数。
代码中的变量解释
结合SQL和源码分析其中的变量的意思:

resultValue:样本计算结果
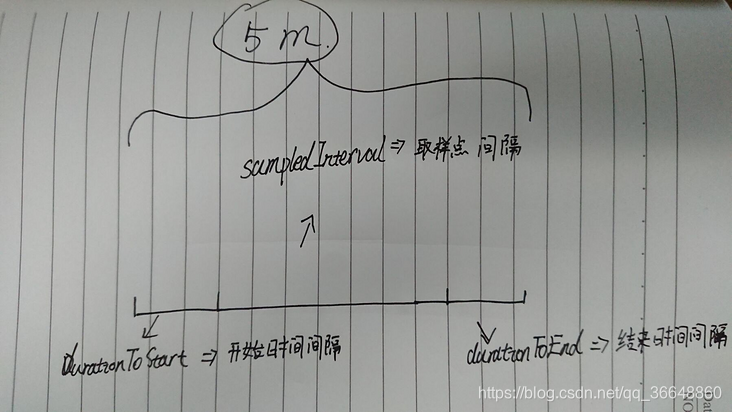
durationToStart:第一个取样时间点到5分钟取值区间的边界起点的时间间隔
durationToEnd:最后一个取样时间点到5分钟取样区间边界终点的时间间隔
sampledInterval:两个取样点时间点之间的时间间隔
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RytKjbsY-1618565129872)(/img/bVbLKJv)]
averageDurationBetweenSamples:取样点时间点时间平均间隔
extrapolationTreshold:取样时间点假定的取样时间区间,这里是假设的取样区间(通过以往的样本点时间区间乘以1.1来推算出一个假定的时间间隔)
extrapolateToInterval:取样时间点的时间区间
看到源码中有一行,发现开始increase()的结果确实resultValue就是两值相减

但是下面代码中还增加了一段外推算法来预判趋势
来看这一段

因为increase()的取值点间隔与真实的5m取样时间区间还是存在两个时间间隔的,也就是durationToStart和durationToEnd,而这两个时间间隔是在计算之外的,也就是说数据采集之间存在空白期,所以采集到的值只能算是一个低精度的近似值。Prometheus在这里使用了数学里的外推法(外推法:在数学里常用的数据精加工方法,通过以最近若干时期的平均值为基础,来计算预测期预期值,把低精度近似值加工到高精度的近似值的一种方法)假定在durationToStart和durationToEnd它就存在增量,用外推法减小每两个取样区间的durationToStart和durationToEnd这两个空白期里的可能存在的增量的误差。
如果空白期内真的存在增量,在这种情况下单纯的只靠取样点之差来构建曲线,数据并不准确的,所以设计团队通过将取样的差值乘以时间间隔之比来求得一个近似值:resultValue * (extrapolateToInterval / sampledInterval),但是如果不存在增量,那么结果可能有偏差,这个结果只能算作一个高精度的“近似值”。
Prometheus假定了一个区间averageDurationBetweenSamples * 1.1,判断这个空白期是否过大,如果过大则需要一个更大的数字来求得近似值,比如一种情况,在durationToStart和durationToEnd都小于外推推算时间间隔时,则间隔较小:durationToStart + durationToEnd + sampledInterval) / sampledInterval * resultValue取值;另一种情况,在durationToStart和durationToEnd都大于外推推算时间间隔时,则间隔过大:(averageDurationBetweenSamples + sampledInterval) / sampledInterval * resultValue,这个值推算出来则可能比第一种情况更大。
这个外推算法也是为什么会出现小数点和与真实值存在误差的原因。
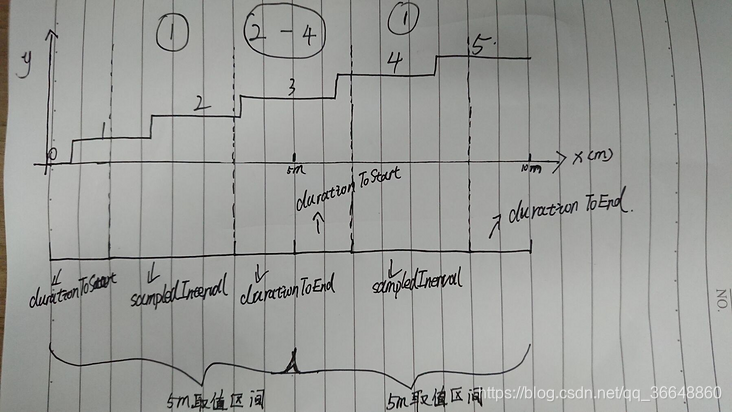
就如下图为例,在两个取样区间零界点前后分别有一个durationToStart和durationToEnd,而这两个时间间隔实际上是increase()函数计算的的空白期。假定没有外推算法,increase()在这两个5分钟的取值区间内获取到的增量应该是总共是1+1=2,而真实增量则是1+2+1=4,在durationToStart和durationToEnd区间内值发生了变化(2到4)。所以如果只是单纯的把取样区间内,最后一个取样值减去第一个取样值是不准确的,无法计算到这个空白期内的增量的,所以需要外推法来做一个趋势的预判得出一个更大一点的近似精确的值,使得结果更加接近真实值。
不得不说不愧是大牛团队,考虑到存在空白时间区间的误差,通过数学的外推法预算出一个近似值来弥补取值过程中的漏取来弥补图形不精确的问题,不过这也造成了一些其他的问题,总的来说Prometheus的强大时毋庸置疑的,从它的设计到功能都非常巧妙,这里要说明的是,依据我个人的实际使用经验来看,Prometheus的采样的数据可能不是准确的值,是一个近似的精确值,各位在使用的时候还是得谨慎呀!
GitHub源码:
本文来自:CSDN博客
感谢作者:CSDN博客
查看原文:【精选】Prometheus源码分析-increase()函数踩坑记_prometheus increase 小数_FrankenFunc `的博客